De ‘levenslijn’ van Christiaan Huygens 

Christiaan Huygens schreef in 1669: 

‘… door het trekken van een kromme lijn, waarop ik met den passer het leven afmeet van elken willekeurigen persoon, [zie ik] b.v. dat gij, op uw leeftijd van 38 jaar, nog ongeveer 19 jaren en 4 maanden leven kunt’¹  

Met deze woorden introduceerde Christiaan het wonderlijke hulpmiddel dat hij gebruikt had om te voorspellen hoe oud zijn broer Lodewijk zal worden. In een brief aan Lodewijk schreef hij dat hij een ‘zeer vertrouwbaar en zeer gemakkelijke’ methode heeft gevonden waarvoor hij geen één moeilijke berekening hoefde te doen. Hij doopte zijn hulpmiddel zelf tot levenslijn. Of zoals wij nu zouden zeggen: een grafiek. 

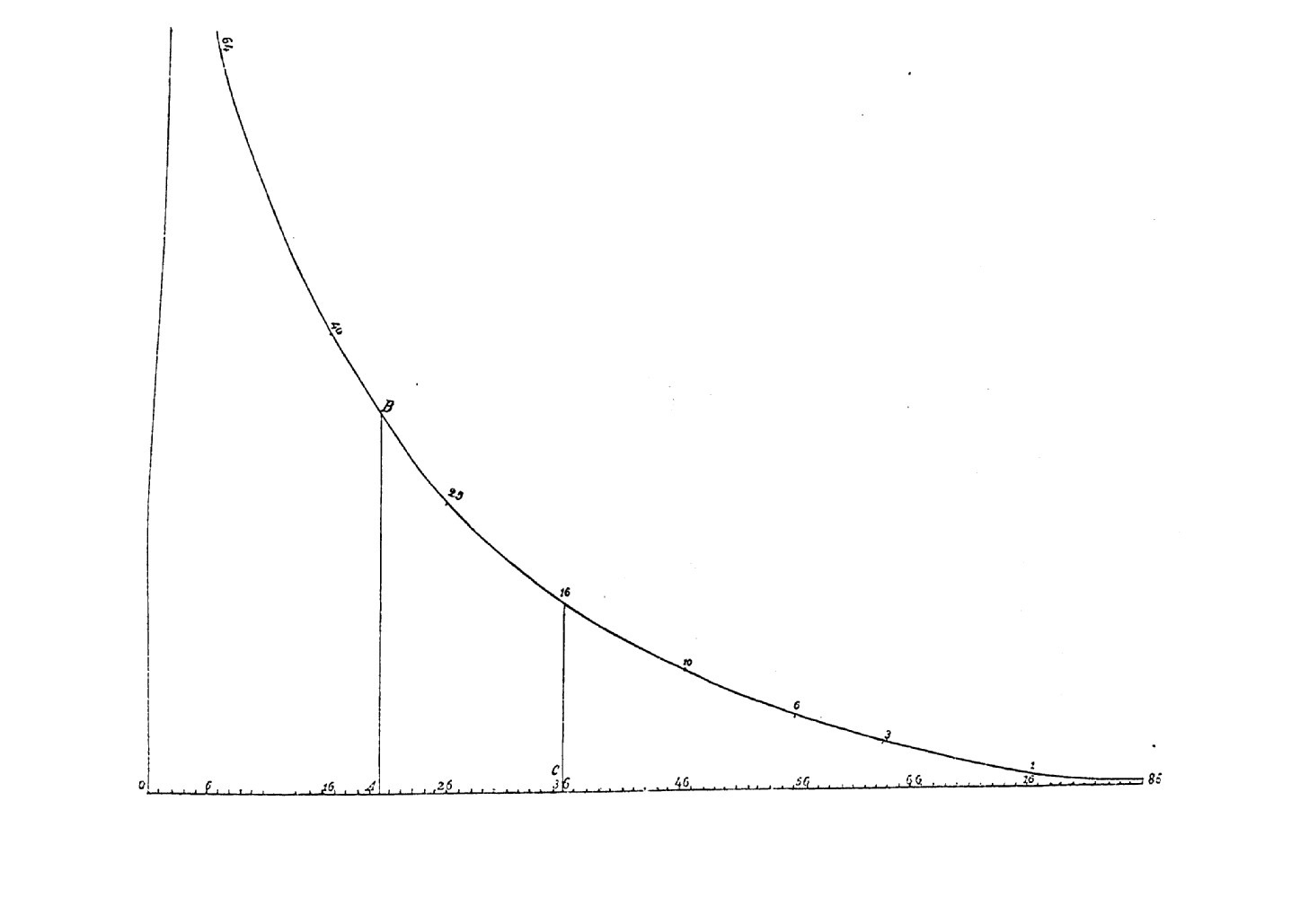
Wie tegenwoordig naar de grafiek hierboven kijkt, zal deze waarschijnlijk vrij gemakkelijk kunnen begrijpen. De grafiek bestaat uit een horizontale rechte lijn met daarop de leeftijden tussen 0 en 85 aangegeven. De kromme lijn daarboven laat zien hoeveel personen van de startgroep van 100 personen er op een bepaalde leeftijd nog in leven zijn.² Door verticale verbindingslijnen te trekken tussen deze twee lijnen kun je bijvoorbeeld aflezen dat er 16 personen zijn die een leeftijd van 33 jaar zullen bereiken, zoals de meest rechter horizontale lijn aangeeft.

Voor de broers Christiaan (1629-1695) en Lodewijk Huygens (1631-1699) was de betekenis van sterftedata en grafieken zoals deze een stuk minder vanzelfsprekend. In de zeventiende eeuw begonnen verschillende wiskundigen na te denken over kansrekening, vooral voor kaart- en dobbelspellen, maar vanwege het gebrek aan beschikbare data kunnen we dan nog niet echt spreken over statistiek. Wel realiseerden enkele landsbestuurders en staatsverzekeraars zich dat het nuttig kon zijn om sterftecijfers bij te houden. Dat leidde tot de eerste eenvoudige sterftetafels. De bekendste hiervan was tabel van de Engelse koopman John Graunt uit 1662.³ Zoals te zien in figuur 2 geeft Graunt voor 100 startpersonen aan hoeveel van hen er op verschillende leeftijden nog in leven zullen zijn. Graunts tabel zou lange tijd functioneren als de standaardtabel voor sterfteverwachting. Hoewel er dus vanaf halverwege de zeventiende eeuw statistische sterftetabellen in omloop waren, geldt dat niet voor sterftegrafieken. Pas twee eeuwen later werd het gebruikelijk om statistische gegevens met lijnen weer te geven.⁴ Sterftecijfers in tabellen zijn historisch gezien dus wat anders dan sterftecijfers in grafieken.

Wat Huygens’ grafiek uitzonderlijk maakt is dat hij bijna tegelijk met de eerste sterftetabellen verscheen, dus bijzonder vroeg. Van dergelijke grafieken zijn er heel weinig andere bekend, zo niet geen.⁵ Gelukkig legde Christiaan – juist omdat zijn grafiek zo ongebruikelijk is – nauwkeurig aan Lodewijk uit waarom hij zijn ‘levenslijn’ had opgesteld en hoe deze gebruikt zou moeten worden. Dat is interessant omdat het ons meer inzicht verschaft in Huygens’ ideeën over het opstellen en toepassen van deze grafiek. Ik zal in dit stuk Christiaan Huygens’ grafische methode blootleggen.

Ik toon daarnaast nog twee andere dingen aan. Ik laat zien dat Christiaan Huygens in de grafiek kansrekening liet samenkomen met analytische meetkunde. Die vakgebieden waren beide nieuwe wiskundige velden in de zeventiende eeuw. Christiaan heeft beide uitgebreid bestudeerd, maar meestal als weinig overlappende vakgebieden. Ik beargumenteer dus dat de grafiek het resultaat is van juist de raakpunten die Huygens wist te vinden tussen beide wiskundige velden. Mijn laatste punt gaat over deze grafiek binnen de verdere briefwisseling. Ik zal laten zien dat de grafiek een cruciale rol speelt in de totstandkoming van een definitie voor ‘verwachtingswaarde’, waar tussen Christiaan en Lodewijk in de briefwisseling een miscommunicatie over bestaat. De briefwisseling is een belangrijke episode in de geschiedenis van de kansrekening omdat dit begrip door hun discussie een heldere betekenis krijgt. De grafiek speelt daar een wezenlijke rol in.  

De broers & de briefwisseling

Tijd voor een korte introductie van Christiaan en Lodewijk Huygens. Als zoons van dichter en diplomaat Constantijn Huygens (1596-1687) groeiden de broers op in een zeer welgesteld gezin. Ze kregen dan ook een uitgebreide opleiding. Lodewijk studeerde rechten en bekleedde daarna vooral diplomatieke en ambtenarenfuncties. Christiaan wendde zich tot de wetenschappen en ontwikkelde zich tot een voorname natuur- en wiskundige. Hij volgde onder andere lessen van de wiskundigen Johan Stampioen en Frans van Schooten jr., de vertaler van Descartes’ Géométrie naar het Latijn.⁶ Via Van Schooten maakte Christiaan kennis met de nieuwe analytische meetkunde. Er zijn meer lijntjes tussen Christiaan Huygens en Descartes, want ook vader Constantijn was goed bevriend met Descartes.⁷

Naast de analytische meetkunde hield Christiaan zich bezig met kansrekening. Hij is daarin vooral bekend geworden vanwege de publicatie van het belangrijke boek De Ratiociniis in Ludo Aleae (‘Van Rekeningh in Spelen van Geluk’, 1657). In zijn tijd bestond de kansrekening vooral uit berekeningen over dobbel- en kansspelen. Huygens verzorgde de eerste streng wiskundige, axiomatische benadering hiervan. Minder bekend is dat hij naast dit boek ook brieven over kansrekening heeft geschreven aan zijn broer Lodewijk.⁸ Die onbekendheid is zonde, want de brieven geven een interessant en persoonlijk inkijkje in de geschiedenis van de kansrekening en statistiek. Zoals Ida Stamhuis elders heeft beargumenteerd laat de briefwisseling zien dat wiskundige concepten niet het resultaat zijn van knap denkwerk van een geïsoleerd individu, maar met vallen en opstaan ontstaan uit een proces van sociale afstemming.⁹

De eerste brief over dit onderwerp komt uit augustus 1669, toen Lodewijk schreef dat hij recent een Engelse sterftetafel onder ogen had gekregen. Het blijkt de hierboven genoemde standaardtabel van John Graunt (die uit figuur 2), die zeven jaar eerder gepubliceerd was.¹⁰ Wat Lodewijk vooral interessant vond, was dat hij met de tabel kon berekenen ‘hoelang personen van allerlei leeftijd nog te leven hebben.’ Preciezer gezegd bedoelt hij daarmee het volgende:

‘De vraag is: hoelang heeft een kind, van den oogenblik af dat de moeder daarvan zwanger is, nog te leven volgens den gewonen gang der natuur? En verder hetzelfde voor iemand van 6 jaar, dan voor een van 16 jaar, van 26 jaar, enz.’¹¹

Deze berekeningen vond Lodewijk niet alleen ‘zeer vermakelijk,’ maar ook ‘nuttig bij het berekenen van Lijfrenten.’¹² Lijfrenten werden in de zeventiende eeuw een populaire manier van verzekeren (en bestaan nog steeds). Bij deze vorm van verzekeren ontving de verzekerde periodieke uitkeringen die zich bleven herhalen zolang het verzekerde ‘lijf’ nog leefde. Dat kan het eigen lijf van de verzekerde zijn, maar het was ook gebruikelijk om de verzekering af te sluiten op het lijf van een jong kind. Om een gunstige verzekering af te sluiten was het dus belangrijk om goed te kunnen inschatten hoelang een lijf nog zou leven.¹³ Lodewijk realiseerde zich dat de sterftetabel hierbij goed van pas zou komen.

Lodewijk besloot Christiaan te schrijven omdat hij dacht dat Christiaan het onderwerp interessant zou vinden, maar ook omdat Lodewijk het rekenwerk zelf best moeilijk vond. ‘Dat zal met u wel niet het geval zijn,’ schrijft hij. Lodewijk durfde namelijk wel toe te geven dat Christiaan van hen tweeën de betere wiskundige was. Om het probleem aan Christiaan te verkopen, verpakte hij het als een raadsel. Hij gaf niet zijn eigen rekenmethode bloot (al was die ‘stellig goed,’ blufte hij). In plaats daarvan gaf hij alleen de resulterende voorspelling waar hij op uitkwam: ‘Volgens mijne berekening zult gij ongeveer 56 en een half jaar oud worden, en ik 55.’¹⁴ 

Lodewijks opzet slaagde en Christiaan antwoordde al binnen een week, ook al moest de brief helemaal naar Christiaans woonplaats Parijs afreizen. Maar uit Christiaans antwoord blijkt vooral dat hij niet onder de indruk was van Lodewijks gewaagde voorspelling.¹⁵ Christiaan meende op basis van de tabel niet te kunnen voorspellen hoe oud de broers zouden worden. Hij dacht slechts te kunnen concluderen dat een moeder een onvoordelige weddenschap zou aangaan als zij zou wedden dat haar kind 16 jaar oud zou worden. Alle andere conclusies die Lodewijk meende te kunnen trekken moeten wel onjuist zijn, want daarvoor was de tabel niet compleet genoeg. ‘[A]ls die berekening op juistheid zal aanspraak maken, dan zou men een tafel moeten bezitten die jaar voor jaar aanwees hoeveel personen er sterven van een ondersteld aantal, b.v. honderd,’ schreef Christiaan. Of anders ‘moet gij die [tabel] door het een of ander middel, zooals ik er een weet, hebben aangevuld.’

Deze opmerking was de eerste referentie naar de grafiek die Christiaan drie maanden later zou opsturen naar zijn broer. Hoewel hij de grafiek niet meestuurde en deze niet eens echt benoemt, toont deze opmerking dat Christiaan al gelijk bij het onder ogen krijgen van Graunts sterftetafel een schets moet hebben gemaakt.

Het probleem dat Christiaan schetste in zijn brief is dat van interpolatie (in moderne termen): zonder beschikking te hebben over volledigere gegevens, wat is dan de juiste manier om de tabel aan te vullen? Net als Lodewijk gaf ook Christiaan zijn ideeën niet gelijk bloot. Wél maakte hij duidelijk dat hij enthousiast was om er verder mee aan de slag te gaan. ‘Ik heb er wel zin in om de tafel aan te vullen, zooals ik gezegd heb, en de vraagstukken op te lossen die men over dit onderwerp, dat nog al ingewikkeld is, kan stellen.’ Hij sloot af met het verzoek aan Lodewijk om zijn rekenwerk uit de doeken te doen: ‘Uwe methode is zeker niet dezelfde als de mijne, en ik zou haar gaarne willen zien. Vaarwel.’

De wiskunde

Tot zover had noch Christiaan, noch Lodewijk zijn methode dus beschreven. Dat veranderde gelukkig in een volgende brief, al reageerde Lodewijk pas twee maanden na dato. Eind oktober werkte Lodewijk zijn rekenmethode uitgebreid uit. Die methode hield het volgende in (pak de sterftetafel uit figuur 2 er voor het gemak vooral bij).

Volgens de tabel zijn er 36 personen die stierven vòòr hun zesde levensjaar. We weten niet precies wanneer zij zijn gestorven, maar gemiddeld hebben zij 3 jaar geleefd. Samen is dat dus 36 x 3 = 108 jaar. Evenzo hebben de 24 personen die tussen hun zesde en zestiende levensjaar stierven gemiddeld 11 jaar geleefd, dus dat levert 24 x 11 = 264 jaar op. Zo doorrekenend komt Lodewijk op een totaal van 1822 bereikte levensjaren. Zijn optelling is ook te zien in figuur 3. Door deze 1822 jaar vervolgens te delen door het totaal van 100 personen, berekende Lodewijk dat de te verwachten sterfteleeftijd van een pasgeborene 1822/100 = 18,22 jaar moest zijn.

Op soortgelijke manier kon Lodewijk ook uitrekenen hoeveel jaar Christiaan en hijzelf nog konden verwachten te leven. We zagen net dat hij de levensverwachting voor pasgeborenen berekende door de 1822 levensjaren jaren uit de tabel te delen door het totaal van 100 personen. Dat werkt ongeveer hetzelfde voor mensen die al ouder zijn dan een pasgeborene. Ook nu kon hij namelijk het totaal aantal nog te leven jaren van de mensen met leeftijden van precies 6, 16, 26, … delen door het totaal aantal personen dat dan nog in leven is (dat zijn niet de initiële 100 mensen maar minder).

Neem ter illustratie iemand van 46. Uit de tabel kunnen we het totaal aantal verwachte levensjaren halen: (4 x 51) + (3x 61) + (2 x 71) + (1 x 81) = 610 jaren. Er zijn er nog 10 in leven, dus de levensverachting is 610/10 = 61 jaar. Voor een 46-jarige is dat dus nog 15 jaar. Voor personen met leeftijden die niet eindigen op een ‘6’ berekende hij de aanstaande levensjaren naar verhouding.¹⁶ Dat was ook het geval voor Christiaan en hemzelf.

Lodewijks berekeningen laten zien dat hij ervan uitging dat de sterfte binnen elke leeftijdsgroep evenredig over de leeftijden is verdeeld. Hij rekende namelijk op basis van de gemiddelde bereikte leeftijd van elke leeftijdscategorie, dus alsof de vier mensen die stierven tussen hun 46^e en 56^e levensjaar ‘gemiddeld’ 51 jaar waren geworden. Zijn manier om de tabel aan te vullen is wat we tegenwoordig een lineaire interpolatie zouden noemen. Op die manier kon Lodewijk uit de voeten met de schaarse waarden uit de tabel.

Toch was het misverstand over levensverwachting nog niet direct opgehelderd nadat Lodewijk zijn methode beschreef. Lodewijk beweerde namelijk dat je een levensduur van 18,22 jaar zou verwachten, terwijl Christiaan vond dat het al onvoordelig was om te wedden dat een pasgeborene 16 jaar zou worden. Hoe rijmt dat met elkaar?

Christiaan was degene die het eerst doorzag wat de miscommunicatie veroorzaakte. Hij had Lodewijks berekeningen goed bekeken en zijn eigen berekeningen nog eens over gemaakt (want die was hij ondertussen alweer kwijtgeraakt, schreef hij). Uit Christiaans volgende brief blijkt dat hij had ontdekt dat Lodewijk sprak over de gemiddelde verwachte leeftijd, terwijl hijzelf de leeftijd had berekend die precies de helft van de mensen wel zal bereiken en de andere helft niet. Lodewijks espérance is wat we tegenwoordig de verwachtingswaarde van de levensduur zouden noemen, terwijl we Christiaans uitkomst nu herkennen als de mediaan van de levensverwachting. Dat die waarden nogal uiteen liepen kwam door de hoge kindersterfte in die tijd. Verder schreef Christiaan dat Lodewijks methode dan wel handiger werkte voor het berekenen van lijfrentes, maar dat zijn eigen methode bruikbaarder was voor de mensen die wilden wedden (en dus volgens de gebruiken van de kansrekening van die tijd). 

De grafiek

Hoog tijd om naar Christiaans interpolatie te kijken, die hij als reactie op Lodewijks uitwerkingen uit de doeken deed. Nu komt eindelijk de grafiek in beeld. Christiaans aanpak was namelijk om de ‘kleine Engelsche tafel’ aan te vullen middels een kromme.¹⁷ Hoe heeft Christiaan die grafiek opgesteld? En hoe kon die worden ingezet om te bepalen hoe lang iemand van een willekeurige leeftijd nog zal leven?

Christiaan volgde Graunts tabelwaarden en ging uit van een startgroep van 100 personen. Die personen representeerde hij met een verticaal lijnstuk. Christiaan schreef dat hij vervolgens op ‘de rechte lijn aan de voet dezes’, dus de lijn die horizontaal loopt, alle mogelijke leeftijden had aangegeven. Door gebruik te maken van verhoudingen kon elk van de waarden uit de tabel nu óók worden opgevat als een lijnstuk loodrecht op de horizontale lijn:

‘[W]aar het cijfer 6 staat is een loodlijn opgericht die 64 deelen bevat, omdat er, volgens de Engelsche tafel, van 100 personen nog 64 op den leeftijd van 6 jaren over zijn.’¹⁸

Zo stelde Christiaan dat alle waarden uit de tabel gerepresenteerd kunnen worden door loodlijnen met lengten naar verhouding. Vervolgens trok Christiaan een kromme lijn door de punten aan het einde van die loodlijnen. Die kromme lijn is wat hij de ‘levenslijn’ noemde. Op deze manier heeft hij de discrete tabelwaarden nu omgezet in een continue verdeling.

Met Christiaans continue levenslijn kon hij een inschatting maken van de sterftegegevens die niet in Graunts tabel voorkwamen. Hoe dat aflezen precies werkt legde Christiaan gedetailleerd uit aan Lodewijk. Stel bijvoorbeeld dat je wilt weten hoeveel personen er nog in leven zijn op hun 20^e jaar. Dat staat niet in de tabel, want die geeft alleen 16 en 26. Je stelt dus een loodlijn op in het punt voor 20-jarigen (punt A in figuur 1) en kijkt waar die loodlijn snijdt met de kromme (punt B). De verhouding tussen de meest linker lijn en AB, ‘die op de schaal der andere lijnen afgemeten 33 deelen uitmaakt,’ vertelt je dus dat er 33 van de 100 personen een leeftijd van 20 jaar zal bereiken. Zo kon Christiaan de sterftetafel aanvullen voor welke leeftijd dan ook.

Op soortgelijke manier kon hij ook vinden hoe lang die 20-jarige nog kan verwachten te leven. Ter herinnering: voor Christiaan, die dacht aan de mediane levensduur, gaat die vraag om het vinden van de leeftijd die de helft van de 20-jarigen wél zal bereiken en de andere helft niet. Om die leeftijd te vinden neem je de helft van de reeds gevonden lengte AB en kijk je vervolgens waar deze onder de kromme past. Zo vond hij lijn CD in de grafiek, die hoort bij 36 levensjaren. De 20-jarige kan dus verwachten 36 jaar oud te worden, nog 16 jaar. Deze methode werkt voor elke gegeven leeftijd. Ook suggereerde Christiaan dat zijn methode gebruikt kan worden om gezamenlijke sterftekansen van meerdere personen uit te rekenen.

Natuurlijk had Christiaan al deze berekeningen ook kunnen doen zonder grafiek. Maar juist door de gegevens uit de tabel ook in een grafiek te plaatsen, worden de verschillende ideeën van de broers over verwachtingswaarde tastbaar. Doordat Christiaan namelijk het aantal mensen visualiseerde als lijnstuk en op zoek ging naar een lijnstuk dat half zo lang is, kreeg de mediaan een concrete betekenis (al bestond het woord ‘mediaan’ natuurlijk nog niet). De grafiek was een essentieel onderdeel om zijn methode begrijpelijk te maken voor Lodewijk. Het was natuurlijk extra mooi geweest als Christiaan ook aan zou geven hoe een grafiek van Lodewijks interpolatie eruit zou zien, maar dat deed hij niet (in die grafiek zouden de toppen van de loodrechte lijnstukken verbonden moeten worden door rechte lijnen in plaats van een vloeiende kromme).

Conclusie

Wat maakt deze grafiek bijzonder? Ik denk dat daar meerdere antwoorden op zijn. Ten eerste is het opmerkelijk dat Christiaan Huygens bij het zien van Graunts sterftetafel gelijk dacht aan een grafiek. Zoals gezegd worden sterftetafels in de zeventiende (en later achttiende) eeuw steeds belangrijker, maar gaat dat niet op voor sterftegrafieken. Die verschenen eigenlijk pas in de negentiende eeuw. Christiaan ontwikkelde deze grafiek dus uitzonderlijk vroeg. Dat deze grafiek ook voor de broers een onbekend fenomeen was blijkt bovendien uit Christiaans gedetailleerde uitleg. Toch ziet hij direct de waarde in van zijn ‘zeer vertrouwbaar en zeer gemakkelijke’ methode.

Ten tweede geeft de grafiek inzicht in de samenhang tussen kansrekening en Cartesiaanse analytische meetkunde in de zeventiende eeuw, twee nieuwe en ogenschijnlijk afzonderlijke wiskundige vakgebieden. Christiaan combineerde ideeën uit beide disciplines bij het opstellen van de grafiek. Dit toont dat deze nieuwe vakgebieden in die tijd niet strikt gescheiden waren, maar dat daar ook raakvlakken tussen bestonden.

Mijn derde en laatste punt is dat de grafiek een wezenlijke rol speelde in de totstandkoming van het concept ‘verwachtingswaarde’. Christiaan krijgt meer grip op de verschillende interpretaties die hij en Lodewijk hanteerden doordat hij zowel rekende met getallen als lijnstukken inpaste. De grafiek werkte als een instrument dat zijn wiskundige ideeën tastbaar en inzichtelijk maakte.

Al met al is het zonde dat de wiskundige briefwisseling tussen Lodewijk en Christiaan relatief onbekend blijft, want hij geeft veel interessante inkijkjes in het wiskundig redeneren in de 17^e eeuw.

1. Christiaan Huygens aan Lodewijk Huygens, No. 1777, 21-11-1669.
   Alle besproken brieven tussen Christiaan en Lodewijk zijn 200 jaar na dato gedrukt en gebundeld in Christiaan Huygens’ Oeuvres Complètes vol. 6 Correspondance 1666-1669 (O.C.), 1895, beschikbaar via DBNL (KB, nationale bibliotheek) en Gallica. De meeste brieven zijn in het Frans. De brieven over kansrekening werden twee jaar na deze Franse publicatie vertaald in het Nederlands door de Algemeene Maatschappij van Levensverzekering en Lijfrente, die ze opnam in Bouwstoffen voor de geschiedenis van de levensverzekeringen en lijfrenten in Nederland, 1897. Alle citaten zijn afkomstig uit deze vertaling, maar eventuele nadruk (schuin) is van mijn hand. ↩︎
2. De 100 initiële personen zijn eigenlijk geen ‘pasgeborenen’, omdat ook de kinderen die overlijden bij de bevalling zijn opgenomen in de gegevens. ↩︎
3. Graunt, Natural and Political Observations … Made upon the Bills of Mortality. ↩︎
4. Friendly and Wainer, A History of Data Visualization and Graphic Communication, 158. ↩︎
5. Er zijn eerder twee korte artikelen van elk twee pagina’s verschenen over de grafiek, in 1947 en 1970. Hierin wordt Huygens’ grafiek vergeleken met een grafiek van d’Alembert een eeuw later, en wordt de context van Graunts tabel verder uitgewerkt. Boyer, ‘Note on an Early Graph of Statistical Data (Huygens 1669)’; White and Hardy, ‘Huygens’ Graph of Graunt’s Data’. ↩︎
6. Descartes ontwikkelt de analytische meetkunde in zijn Géométrie (1637), waarin hij laat zien hoe meetkundige vormen kunnen worden gebruikt om algebraïsche vergelijkingen te beschrijven en op te lossen. Vandaar dat we spreken over een ‘Cartesisch’ coördinatenstelsel. ↩︎
7. Constantijn Huygens en René Descartes schreven elkaar onder andere over de leraar die Constantijn moest aanstellen voor zijn zoons. Descartes heeft hem toen geadviseerd om Van Schooten te benaderen (Descartes schrijft: ‘… want ik ken niemand in dit land, en nauwelijks iemand elders, die zo bekwaam is [in de algebra] als hij.’). Christiaan Huygens, Oeuvres Complètes, vol. 1 1638-1656, H. Bruno aan Constantijn Huygens sr., No. 3b, 17-06-1643, beschikbaar via DBNL of vertaald hier. ↩︎
8. Al worden de brieven in een paar overzichtswerken wel genoemd, zoals Hald, A History of Probability and Statistics and Their Applications before 1750; Hacking, The Emergence of Probability; Daston, Classical Probability in the Enlightenment. ↩︎
9. Stamhuis, ‘Christiaan Huygens correspondeert met zijn broer over levensduur. Hoe wetenschappelijke begrippen kunnen ontstaan’. ↩︎
10. De broers zijn zich bewust dat hun berekeningen slechts benaderingen zullen blijven. Lodewijk schrijft dat de ‘bewerker’ van de tabellen (Graunt) dat zelf heeft toegegeven. Maar hoewel de tafel geen aanspraak maakt op ‘volkomen juistheid,’ liggen de waarden ‘voor de praktijk na genoeg bij de waarheid, want de menschen sterven niet volgens nauwkeurige verhoudingen, en evenmin volgens gebroken getallen.’ Lodewijk Huygens aan Christiaan Huygens, No. 1771, 30-10-1669. ↩︎
11. Lodewijk Huygens aan Christiaan Huygens, No. 1755, 22-08-1669 ↩︎
12. Lodewijk Huygens aan Christiaan Huygens, No. 1755, 22-08-1669.  ↩︎
13. Voor meer over lijfrentes in Nederland, zie Hogendijk, ‘Lijfrentes in de zeventiende en achttiende eeuw’. ↩︎
14. Lodewijk Huygens aan Christiaan Huygens, No. 1755, 22-08-1669. ↩︎
15. Christiaan Huygens aan Lodewijk Huygens, No. 1756, 28-08-1669.  ↩︎
16. Lodewijk Huygens aan Christiaan Huygens, No. 1771, 30-10-1669. De berekening is ook beschreven in Stamhuis, ‘Christiaan Huygens correspondeert met zijn broer over levensduur. Hoe wetenschappelijke begrippen kunnen ontstaan’. ↩︎
17. Christiaan Huygens aan Lodewijk Huygens, No. 1776, 21-11-1669. ↩︎
18. Christiaan Huygens aan Lodewijk Huygens, No. 1776, 21-11-1669. ↩︎